モンテカルロシミュレーション

収益評価の基本のキ（第８回）
ＤＤＣＦ法②

藤井和之
株式会社タス

ＤＤＣＦ法における将来の収益の算出の核となるのが、モンテカルロシミュレーションです。

モンテカルロシミュレーションはある確率分布（※１）に従った乱数と確率過程モデルを用いて、それにより１万回程度の複数の値（パスと呼びます）を算出する方法で、1940年代に原子爆弾の開発計画（マンハッタン計画）において中性子のランダムな動きを解析するためにフォン・ノイマンらによって考案されました。

ちなみにこのフォン・ノイマンという方は『万能の天才科学者』として、物理学や量子力学、数学、経済学、気象学、コンピューター、原爆の基本設計、米国防衛構想に及ぶ広大なジャンルで大きな役割を果たした人物で、現在われわれが利用しているコンピューターの基礎を考案した方でもあります（※２）。

さて、確率過程モデルとは、時間とともに推移する確率現象の数学的モデルです。

代表的なものとして「幾何ブラウン運動モデル」があり、金融の世界ではよく利用されています。ブラウン運動は、1827年にイギリスの植物学者ロバート・ブラウンによって発見されました。水に浮かべた花粉の微粒子がまるで生き物のように震動している現象で、この粒子の運動過程をブラウン運動と呼びます（図１）。理科の授業で習った方も多いと思います。

図１　ブラウン運動

このブラウン運動が作り出す確率過程を数式化したものをウィーナー過程、それに一定の方向性を持たせたものが「幾何ブラウン運動モデル」であり、下記のような式で表されます。

青字で示した部分が一定の方向性を示す部分（ドリフト項と呼びます）、赤字の部分がウィーナー過程です。なお平均と標準偏差は、Xのこれまでの動きから算出します。

幾何ブラウン運動モデルは、「酔っ払いの千鳥足」に例えられます。

酔っ払いの千鳥足は、家に向かう動きとフラフラする動きからなっていますが、酔っ払いの程度によってフラフラする足取りが大きくなったり、小さくなったりします。この家に向かう動きがドリフト項、フラフラの動きがウィーナー過程というわけです。そして、次の時点に酔っ払いが到達している場所は確率分布によります（図２）。

このような動きを幾何ブラウン運動モデルと確率分布に基づいた乱数で分析するのが、モンテカルロシミュレーションなのです。

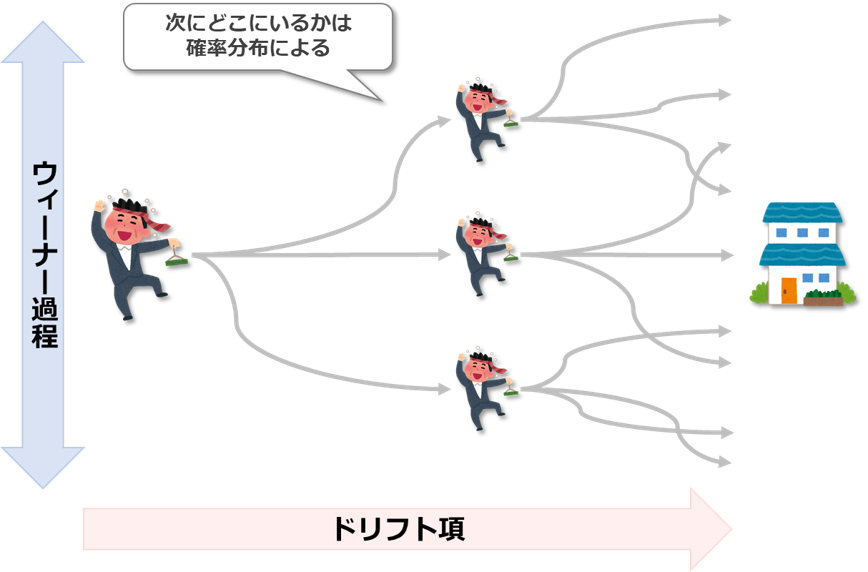
図２　幾何ブラウン運動のイメージ「酔っ払いの千鳥足」

ＤＤＣＦ法では、将来の賃料や空室率をモンテカルロシミュレーションで算出し、１万通り程度のキャッシュフローを算出、それらの収益をＤＣＦ法で計算し価格の分布を算出します。

前回（第７回）、ＤＤＣＦ法はＤＣＦ法よりも詳細なデータを必要とするというお話をしました。

賃料や空室率のウィーナー過程を設定するためには、過去数年にわたる賃料や空室率の時系列データが必要となります。データに基づかないウィーナー過程を用いたモンテカルロシミュレーションは意味がないのです。

次回は、タスが公表している賃料指数や空室率ＴＶＩを利用したＤＤＣＦ法について解説します。

※１：一般的には正規分布が利用されることが多い。
※２：このため、現在のコンピューターはノイマン型と称されています。